Ohm törvénye egy teljes láncra és egy láncszakaszra: a képlet, leírás és magyarázat megírásának lehetőségei

Egy hivatásos villanyszerelőnek vagy elektronikai szakembernek nincs lehetősége arra, hogy saját tevékenysége során megkerülje Ohm törvényét, és megoldja az elektronikus és elektromos áramkörök beállításával, beállításával és javításával kapcsolatos problémákat.

Valójában mindenkinek meg kell értenie ezt a törvényt. Mert az elektromossággal mindenkinek meg kell küzdenie a hétköznapokban.

És bár a német fizikus Ohm törvénye szerepel a középiskolai tantervben, a gyakorlatban nem mindig tanulják meg kellő időben. Ezért anyagunkban megvizsgálunk egy ilyen releváns témát az élet számára, és megértjük a képlet megírásának lehetőségeit.

Egyrészes és teljes elektromos áramkör

Ha figyelembe vesszük az elektromos áramkört az Ohm-törvény áramkörre való alkalmazása szempontjából, két lehetséges számítási lehetőséget kell megjegyezni: egy külön szakaszhoz és egy teljes áramkörhöz.

Az elektromos áramkör szakaszának áramának kiszámítása

Az elektromos áramkör egy szakaszát általában az áramkör azon részének tekintik, amely kizárja az EMF forrását, mivel további belső ellenállással rendelkezik.

Ezért a számítási képlet ebben az esetben egyszerűnek tűnik:

I = U/R,

Ahol, ill.

• én – áramerősség;
• U – rákapcsolt feszültség;
• R - ellenállás.

A képlet értelmezése egyszerű - az áramkör egy bizonyos szakaszán átfolyó áram arányos a rá alkalmazott feszültséggel, az ellenállás pedig fordítottan arányos.

Az úgynevezett grafikus százszorszép, amelyen keresztül bemutatásra kerül az Ohm-törvényen alapuló megfogalmazások teljes variációja. Kényelmes eszköz a zsebes tároláshoz: „P” szektor - teljesítményképletek; „U” szektor - feszültségképletek; „I” szektor - aktuális képletek; szektor „R” - ellenállási képletek

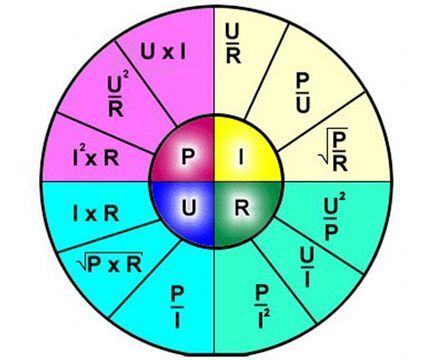
Így a képlet egyértelműen leírja az áram áramlásának függőségét az elektromos áramkör egy külön szakaszán a feszültség és ellenállás bizonyos értékeihez képest.

A képlet kényelmesen használható például az áramkörbe forrasztandó ellenállás paramétereinek kiszámításakor, ha a feszültség és az áram adott.

Ohm törvénye és két következmény, amelyet minden hivatásos elektromechanikus mérnöknek, villamosmérnöknek, elektronikai mérnöknek és bárkinek, aki részt vesz az elektromos áramkörök üzemeltetésében, ismernie kell. Balról jobbra: 1 - áram meghatározása; 2 - ellenállás meghatározása; 3 - a feszültség meghatározása, ahol I - áram, U - feszültség, R - ellenállás

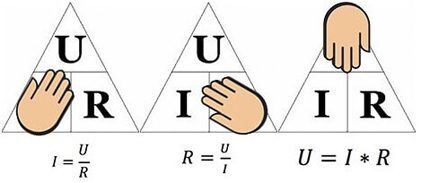
A fenti ábra segít meghatározni például a 10 ohmos ellenálláson átfolyó áramot, amelyre 12 voltos feszültség vonatkozik. Az értékeket behelyettesítve azt kapjuk, hogy – I = 12 / 10 = 1,2 amper.

Hasonló módon oldják meg az ellenállás (ha az áram és a feszültség) vagy a feszültség (ha a feszültség és az áramerősség ismert) megtalálásának problémáit.

Így mindig kiválasztható a szükséges üzemi feszültség, a szükséges áramerősség és az optimális ellenálláselem.

A javasolt képlet nem igényli a feszültségforrás paramétereinek figyelembevételét.Egy például akkumulátort tartalmazó áramkört azonban egy másik képlet alapján számítanak ki. Az ábrán: A – az ampermérő bekapcsolása; V – kapcsolja be a voltmérőt.

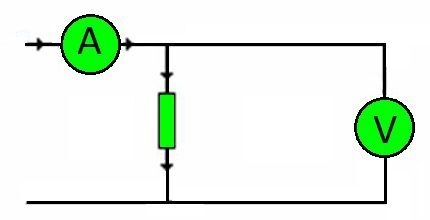
Egyébként bármely áramkör csatlakozó vezetékei ellenállások. Az elviselhető terhelés mértékét a feszültség határozza meg.

Ennek megfelelően, ismét Ohm törvényét alkalmazva, lehetővé válik a szükséges vezeték-keresztmetszet pontos kiválasztása a mag anyagától függően.

Weboldalunkon részletes útmutatás található kábel keresztmetszet számítás teljesítmény és áram tekintetében.

Számítási lehetőség egy teljes lánchoz

A teljes áramkör egy szakaszból (szakaszokból), valamint egy EMF-forrásból áll. Ez azt jelenti, hogy az EMF-forrás belső ellenállása hozzáadódik az áramköri szakasz meglévő rezisztív összetevőjéhez.

Ezért logikus a fenti képlet kissé megváltoztatása:

I = U / (R + r)

Természetesen az EMF belső ellenállásának értéke az Ohm-törvényben egy teljes elektromos áramkörre elhanyagolhatónak tekinthető, bár ez az ellenállásérték nagymértékben függ az EMF-forrás szerkezetétől.

Az összetett elektronikus áramkörök, sok vezetővel rendelkező elektromos áramkörök kiszámításakor azonban a további ellenállás jelenléte fontos tényező.

A teljes elektromos áramkör körülményei között végzett számítások során az EMF-forrás ellenállásértékét mindig figyelembe veszik. Ezt az értéket összeadjuk magának az elektromos áramkörnek az ellenállási ellenállásával. Az ábrán: I - áram áramlása; R – külső ellenálláselem; r az EMF (energiaforrás) ellenállási tényezője

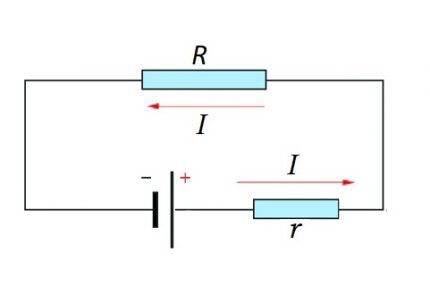
Mind az áramkör egy szakasza, mind a teljes áramkör esetében figyelembe kell venni a természetes pillanatot - állandó vagy változó áramot.

Ha a fent említett, Ohm törvényére jellemző pontokat az egyenáram felhasználása szempontjából vettük figyelembe, akkor a váltakozó árammal minden kissé másképp néz ki.

A törvény változó mennyiségre gyakorolt ​​hatásának figyelembevétele

Az átmenő váltakozó áram feltételeivel szembeni „ellenállás” fogalmát inkább az „impedancia” fogalmának kell tekinteni. Ez a rezisztív terhelés (Ra) és a reaktív ellenállás terhelés (Rr) kombinációjára vonatkozik.

Az ilyen jelenségeket az induktív elemek paraméterei és a kapcsolási törvények okozzák egy változó feszültségértékhez - egy szinuszos áramértékhez.

Ez a váltakozó áramú elektromos áramkör egyenértékű áramköre az Ohm-törvény elvein alapuló formulák felhasználásával történő számításhoz: R - rezisztív komponens; C a kapacitív komponens; L – induktív komponens; Az EMF energiaforrás; I - áramáramlás

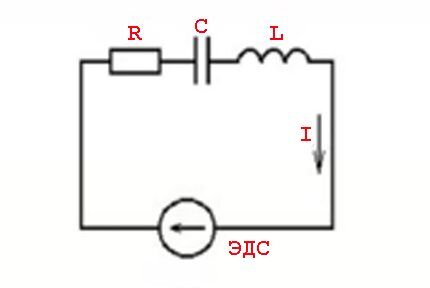
Más szóval, a feszültségértékekből kivezető áramértékek (lag) hatással vannak, amihez aktív (ellenálló) és reaktív (induktív vagy kapacitív) teljesítmények megjelenése társul.

Az ilyen jelenségek kiszámítása a következő képlettel történik:

Z=U/I vagy Z = R + J* (X_L -X_C)

Ahol: Z – impedancia; R – aktív terhelés; x_L , x_C – induktív és kapacitív terhelés; J - együttható.

Elemek soros és párhuzamos csatlakoztatása

Az elektromos áramkör elemei (az áramkör szakasza) esetében jellemző pont a soros vagy párhuzamos csatlakozás.

Ennek megfelelően minden csatlakozástípushoz más-más áram- és feszültségellátási mintázat társul.Ebben a tekintetben az Ohm-törvényt is eltérően alkalmazzák, attól függően, hogy milyen lehetőségek vannak az elemek felvételére.

Sorosan kapcsolt ellenálláselemek áramköre

Soros csatlakozással kapcsolatban (az áramkör két komponensből álló szakasza) a következő megfogalmazást alkalmazzuk:

• én = én₁ = I₂ ;
• U = U₁ +U₂ ;
• R = R₁ + R₂

Ez a megfogalmazás egyértelműen bizonyítja, hogy a sorba kapcsolt rezisztív alkatrészek számától függetlenül az áramkör egy szakaszán átfolyó áram értéke nem változik.

Az ellenállás elemek összekapcsolása az áramkör egy szakaszában egymással sorosan. Ennek az opciónak saját számítási törvénye van. Az ábrán: I, I1, I2 - áram áramlása; R1, R2 - rezisztív elemek; U, U1, U2 - rákapcsolt feszültség

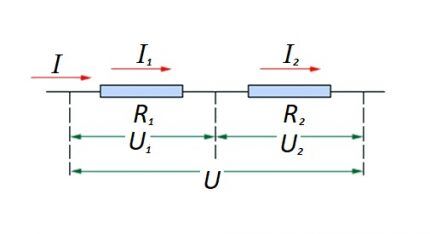
Az áramkör effektív rezisztív összetevőire alkalmazott feszültség nagysága az emf forrás értékének összege és összege.

Ebben az esetben az egyes alkatrészek feszültsége egyenlő: Ux = I * Rx.

A teljes ellenállást az áramkörben lévő összes rezisztív komponens értékének összegének kell tekinteni.

Párhuzamosan kapcsolt ellenálláselemek áramköre

Abban az esetben, ha az ellenállásos komponensek párhuzamosan kapcsolódnak, a következő megfogalmazás tekinthető igazságosnak a német fizikus Ohm törvényéhez képest:

• én = én₁ +I₂ … ;
• U = U₁ =U₂ … ;
• 1/R = 1/R₁ + 1/R₂ + …

Nincsenek kizárva a „vegyes” típusú áramköri szakaszok létrehozásának lehetőségei párhuzamos és soros csatlakozások esetén.

Ellenálló elemek összekapcsolása egy áramkör szakaszán egymással párhuzamosan. Ehhez a lehetőséghez más számítási törvényt kell alkalmazni. Az ábrán: I, I1, I2 - áram áramlása; R1, R2 - rezisztív elemek; U a betáplált feszültség; A, B - belépési/kilépési pontok

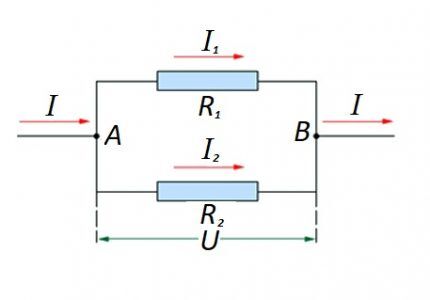
Az ilyen opciók esetében a számítást általában a párhuzamos csatlakozás ellenállásának kezdeti kiszámításával végzik. Ezután a sorba kapcsolt ellenállás értékét hozzáadjuk a kapott eredményhez.

A jog integrál és differenciális formái

A fenti számítási pontok mindegyike alkalmazható olyan körülményekre, amikor úgymond „homogén” szerkezetű vezetőket használnak az elektromos áramkörökben.

Eközben a gyakorlatban gyakran kell vázlatrajzok készítésével foglalkozni, ahol a vezetők szerkezete a különböző szakaszokon változik. Például nagyobb keresztmetszetű, vagy fordítva, kisebb vezetékeket használnak, amelyek különböző anyagokból készülnek.

Az ilyen különbségek figyelembevételéhez létezik az úgynevezett „differenciál-integrál Ohm-törvény” egy változata. Egy végtelenül kicsi vezető esetén az áramsűrűség szintjét a feszültség és a vezetőképesség értékétől függően számítják ki.

A differenciálszámításhoz a következő képletet használjuk: J = ό * E

Ennek megfelelően az integrálszámításhoz a képlet a következő: I * R = φ1 – φ2 + έ

Ezek a példák azonban közelebb állnak a felsőbb matematikai iskolához, és valójában nem használják az egyszerű villanyszerelő gyakorlatában.

Következtetések és hasznos videó a témában

Az Ohm-törvény részletes elemzése az alábbi videóban segít az ilyen irányú ismeretek megszilárdításában.

Egy egyedülálló videóóra minőségileg megerősíti az elméleti írásbeli prezentációt:

A villanyszerelő munkája vagy az elektronikai mérnök tevékenysége szervesen összefügg azokkal a pillanatokkal, amikor ténylegesen be kell tartani Georg Ohm törvényét. Ezek olyan közmondások, amelyeket minden szakembernek tudnia kell.

Ebben a kérdésben nincs szükség kiterjedt ismeretekre - elegendő a megfogalmazás három fő változatának megismerése a gyakorlatban történő sikeres alkalmazáshoz.

Ki szeretné egészíteni a fenti anyagot értékes megjegyzésekkel, vagy kifejtené véleményét? Kérjük, írja meg észrevételeit a cikk alatti blokkba. Ha kérdése van, ne habozzon feltenni szakértőinket.